How To Draw Asymptotes In Matlab

Arrangement construction
Root locus pattern
PID control
What happens to the cart's position?

In this page we will design a controller for the inverted pendulum organization using the root locus blueprint method. In the blueprint process we volition assume a single-input, single-output plant as described by the following transfer office. Otherwise stated, we volition attempt to control the pendulum's bending without regard for the cart'southward position.

(ane) $P_{pend}(s) = \frac{\Phi(s)}{U(s)}=\frac{\frac{ml}{q}s}{s^3+\frac{b(I+ml^2)}{q}s^2-\frac{(M+m)mgl}{q}s-\frac{bmgl}{q}} \qquad [ \frac{rad}{N}]$

where,

(2) $$q = (M+m)(I+ml^2) - (ml)^2$$

More than specifically, the controller will attempt to maintain the pendulum vertically upward when the cart is subjected to a 1-Nsec impulse. Under these conditions, the pattern criteria are:

Settling fourth dimension of less than 5 seconds
Pendulum should not move more 0.05 radians away from the vertical

For the original trouble setup and the derivation of the above transfer role, please consult the Inverted Pendulum: System Modeling page.

System construction

The construction of the controller for this problem is a petty different than the standard control problems you may exist used to. Since nosotros are attempting to control the pendulum's position, which should render to the vertical after the initial disturbance, the reference signal nosotros are tracking should exist aught. This blazon of situation is often referred to every bit a Regulator trouble. The external force applied to the cart can be considered as an impulsive disturbance. The schematic for this problem is depicted beneath.

You lot may find it easier to clarify and design for this system if nosotros commencement rearrange the schematic as follows.

The resulting transfer part $T(s)$ for the closed-loop arrangement from an input of forcefulness $F$ to an output of pendulum angle $\phi$ is then adamant to be the following.

(3) $T(s) = \frac{\Phi(s)}{F(s)} = \frac{P_{pend}(s)}{1 + C(s)P_{pend}(s)}$

Before we begin designing our controller, nosotros showtime demand to define our found within MATLAB. Create a new m-file and type in the following commands to create the constitute model (refer to the main trouble for the details of getting these commands).

1000 = 0.5; chiliad = 0.2; b = 0.1; I = 0.006; g = 9.8; l = 0.iii; q = (M+k)*(I+m*l^2)-(thou*l)^2; due south = tf('s'); P_pend = (m*l*s/q)/(s^3 + (b*(I + g*l^2))*south^2/q - ((M + m)*m*g*l)*s/q - b*m*g*l/q);

Root locus design

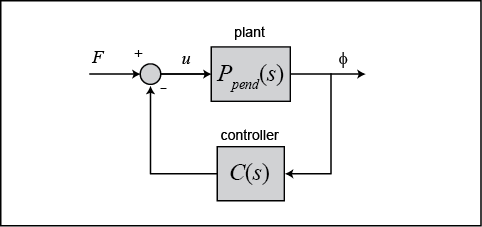
We will at present begin to design a controller for our organization employing a root locus design method. We can employ the MATLAB control rlocus for generating the root locus plots. Calculation the post-obit commands to your 1000-file and running it in the MATLAB command window will create the root locus plot shown below. This plot displays all possible closed-loop pole locations every bit a simple proportional command proceeds $K$ is varied from 0 to infinity. The root locus is the same whether the multiplicative gain $K$ is in the forward or feedback path of the airtight-loop organisation.

rlocus(P_pend) championship('Root Locus of Institute (under Proportional Control)')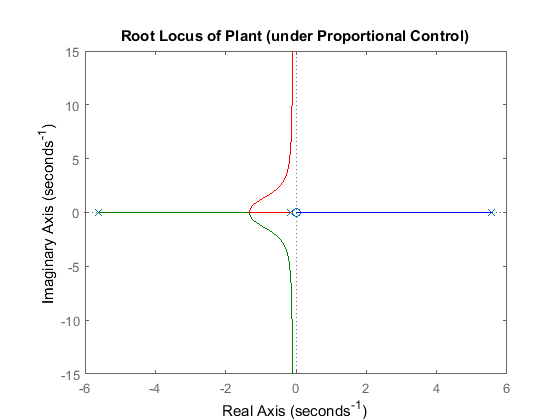

Every bit you lot tin see, one of the branches of the root locus is entirely in the right-half of the circuitous due south-plane. This means that no matter the pick of gain $K$ , there will always be a airtight-loop pole in the right-one-half aeroplane making the system'southward impulse response unstable.

To solve this problem, nosotros need to add together a pole at the origin (an integrator) via the controller to cancel the establish zippo at the origin. This addition will produce two closed-loop poles in the right-half plane. In our subsequent design nosotros tin can then modify our controller to describe these poles into the left-half plane, thereby stabilizing the closed-loop system. Modifying your m-file with the following commands and re-running in the MATLAB command window will produce the root locus plot shown below.

C = 1/s; rlocus(C*P_pend) championship('Root Locus with Integral Command')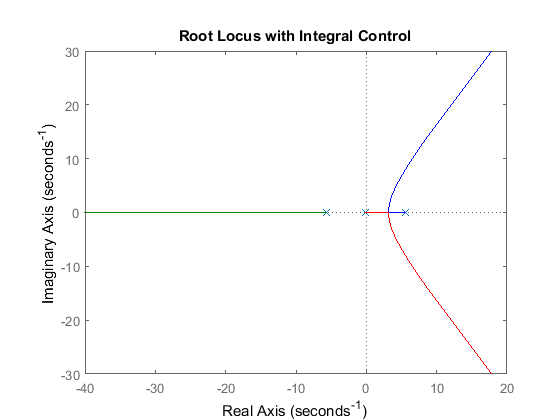

Let's also examine the locations of the organisation's open-loop poles and zeros and so that we may begin to think about how to draw the root locus branches into the left-one-half plane. Entering the following commands into the MATLAB command window will generate the following output.

zeros = zero(C*P_pend) poles = pole(C*P_pend)

zeros =      0 poles =          0     5.5651    -5.6041    -0.1428

As you can run into, there are four poles and only one zero. This means that the root locus volition have three asymptotes: 1 along the real axis in the negative management, and the other two at 120 degree angles to this 1.

This configuration is also unsatisfactory because we still have branches of the root locus that are entirely in the correct-one-half circuitous plane. In general, we can pull the branches of our root locus to the left in the circuitous plane by adding zeros to our arrangement. Adding a zero to our controller volition reduce the number of asymptotes from three to ii. These ii asymptotes will be parallel to the imaginary axis and will intersect the real axis at the location south calculated from the post-obit expression.

(4) $s = \frac{\Sigma poles - \Sigma zeros}{\#poles - \#zeros}$

Therefore, for our system as described so far, nosotros accept the post-obit assuming a minimum-stage null (negative).

(5) $s = \frac{(-5.6041+5.5651-0.1428+0)-(0-z)}{4-2} = \frac{-0.1818+z}{2}$

Based on the above, the farthest we can pull the asymptotes to the left in the complex airplane is approximately -0.1 for a negligibly small zero. Recall that 2% settling time can be estimated from the following equation.

(vi) $T_s = \frac{4}{\sigma}$

Therefore, dominant closed-loop poles with real parts that arroyo -0.1 will non be sufficient to run into the 5 second settling time that nosotros crave.

PID control

In the above discussion we demonstrated that adding a zero to our integral controller could pull the branches of the root locus to the left in the circuitous plane, but nosotros were not able to the pull the dominant branches far enough to the left. A possible solution is to add together yet another zero. If we place both zeros on the negative real axis between the 2 plant poles, then the two branches in the right-half plane volition be pulled into the left-half plane and volition terminate at these two zeros. Let's specifically evaluate the root locus for a controller with an integrator and zeros at -3 and -4. Annotation that this controller is really a PID controller. We tin can create this controller within MATLAB using the zpk command which creates a model by specifying the zeros, poles, and gain of the system. Modifying your m-file with the following commands and re-running volition produce the root locus plot shown below.

z = [-3 -4]; p = 0; k = 1; C = zpk(z,p,k); rlocus(C*P_pend) championship('Root Locus with PID Controller')

Examining the above root locus helps u.s. to determine whether or not our given requirements can be met. Specifically, since it is desired that the settling time of the organization exist less than 5 seconds, the real parts of our dominant closed-loop poles should exist less than approximately -iv/v = -0.8. In other words, our dominatnt closed-loop poles should be located in the complex s-plane to the left of a vertical line at s = -0.viii. Inspection of the above shows that this is possible. Since information technology is also desired that the pendulum not move more than than 0.05 radians abroad from vertical, we likewise desire to ensure that the closed-loop organisation has sufficient damping. Placing the dominant closed-loop poles most the existent centrality will increase the arrangement's damping (pocket-sized $\beta$ ).

To find the proceeds respective to a specific point on the root locus, we can apply the rlocfind command. Specifically, enter the command [one thousand,poles] = rlocfind(C*P_pend) in the MATLAB command window.

Then go to the plot and select a signal on the root locus on left side of the loop, close to the existent axis as shown below with the small + marks. Selecting these poles will ensure that the system settles sufficiently fast and, hopefully, that it has sufficient damping.

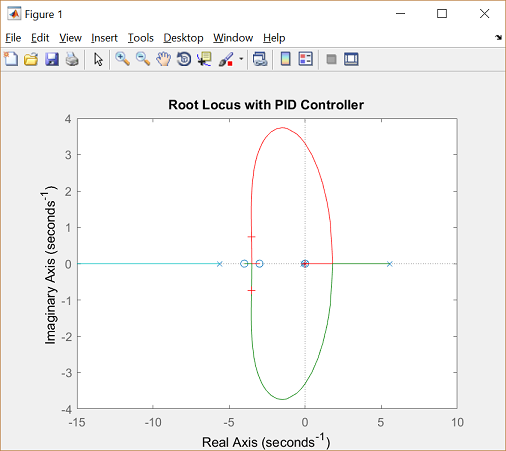
After doing this, you should see an output similar the following in the MATLAB command window.

Select a signal in the graphics window                    selected_point =                    -3.5367 + 0.7081i                              k =                    xx.2396                              poles =                    0          -85.1333          -3.5232 + 0.7086i          -3.5232 - 0.7086i

Annotation that the values returned in your MATLAB command window may non be exactly the same, but they should at least accept the same order of magnitude.

Then we tin can check the impulse response of our closed-loop system to see if our requirements are actually met for a gain $K$ of approximately 20. Add the following commands to your g-file and re-run to generate a closed-loop impulse response like the i shown beneath.

K = xx; T = feedback(P_pend,One thousand*C); impulse(T) title('Impulse Disturbance Response of Pendulum Angle nether PID Control');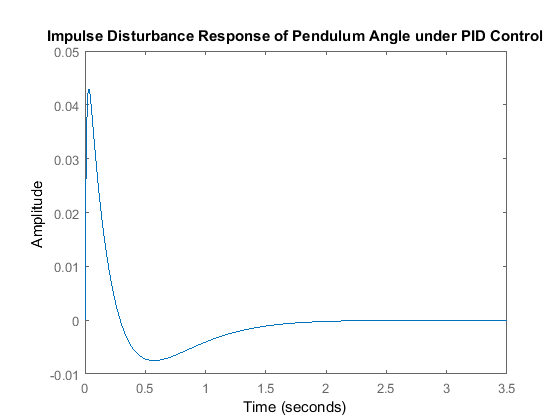

Examination of the above demonstrates that all of the given requirements are met.

What happens to the cart's position?

At the offset of this page, a cake diagram for the inverted pendulum system was given. The diagram was not entirely complete. The block representing the response of the cart's position $x$ was not included because that variable is not beingness controlled. It is interesting though, to see what is happening to the cart's position when the controller for the pendulum'south angle is in place. To come across this we need to consider the full organisation cake diagram every bit shown in the following figure.

Rearranging, we go the following block diagram.

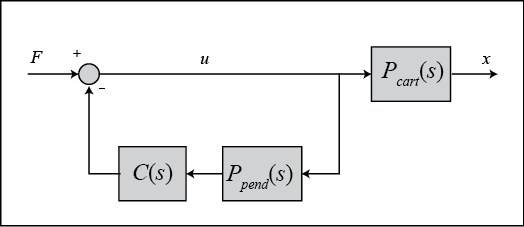
In the higher up, the block $C(s)$ is the controller designed for maintaining the pendulum vertical. The airtight-loop transfer office $T_2(s)$ from an input force applied to the cart to an output of cart position is, therefore, given by the post-obit.

(seven) $T_2(s) = \frac{X(s)}{F(s)} = \frac{P_{cart}(s)}{1 + P_{pend}(s)C(s)}$

Referring to the Inverted Pendulum: System Modeling folio, the transfer part for $P_{cart}(s)$ is defined as follows.

(8) $P_{cart}(s) = \frac{X(s)}{U(s)} = \frac{ \frac{ (I+ml^2)s^2 - gml } {q} }{s^4+\frac{b(I+ml^2)}{q}s^3-\frac{(M+m)mgl}{q}s^2-\frac{bmgl}{q}s} \qquad [ \frac{m}{N}]$

where,

(9) $$q=[(M+m)(I+ml^2)-(ml)^2]$$

Adding the following commands to your g-file (presuming $P_{pend}(s)$ and $C(s)$ are still divers) will generate the response of the cart'due south position to the same impulsive disturbance we have been considering.

P_cart = (((I+m*l^2)/q)*due south^2 - (yard*g*fifty/q))/(s^4 + (b*(I + k*50^2))*s^iii/q - ((M + thou)*yard*g*50)*s^ii/q - b*m*1000*l*s/q); T2 = feedback(1,P_pend*C)*P_cart; t = 0:0.01:8.five; impulse(T2, t); title('Impulse Disturbance Response of Cart Position under PID Control');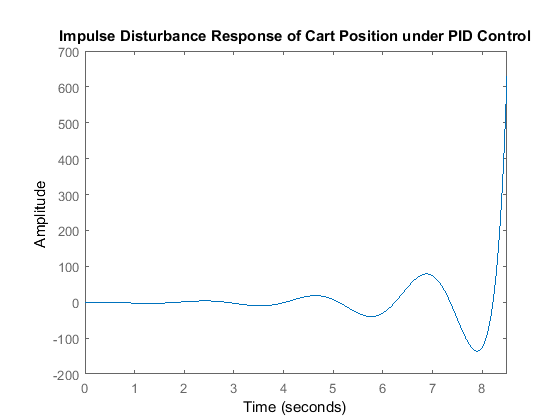

As you lot can come across, the cart's position goes unstable for this impulse disturbance. Therefore, although the PID controller stabilizes the angle of the pendulum, this pattern would not be feasible to implement on an actual physical system.